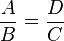Función, relación

Una relación matemática es la correspondencia entre los elementos de dos conjuntos que forman parejas ordenadas

Una función matematica es la correspondencia o relación de cada elemento de un conjunto A con un único elemento del conjunto B. 

"Todas las relaciones son funciones , pero no todas las funciones son relaciones"

teorema de pitagoras

El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de los catetos (los dos lados menores del triángulo, los que conforman el ángulo recto).

Teorema de Pitágoras

"En todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos."

-Pitágoras de Samos 

RAZONES TRIGONOMETRICAS

Razones trigonométricas:

1 Seno

Seno del ángulo B: es la razón entre el cateto opuesto al ángulo y la hipotenusa.

 

 

 

2Coseno

Coseno del ángulo B: es la razón entre el cateto contiguo al ángulo y la hipotenusa.

 

 

 

 

3 Tangente

Tangente del ángulo B: es la razón entre el cateto opuesto al ángulo y el cateto contiguo al ángulo.

 

 

 

 

4 Cosecante

Cosecante del ángulo B: es la razón inversa del seno de B.

 

 

 

 

 

5 Secante

Secante del ángulo B: es la razón inversa del coseno de B.

 

 

 

 

 

 

6Cotangente

Cotangente del ángulo B: es la razón inversa de la tangente de B.

  

      

''HOMOTECIA''

HOMOTECIA

Es la transformación geométrica que no tiene una imagen congruente, ya que a partir de una figura dada se obtienen una o var9ias figuras en tamaño mayor o menor que la figura dada, para obtenerlas se parte de un punto escogido arbitrariamente, al cual se llama centro de homotecia, del cual se trazan segmentos de recta, tantos como vértices tenga la figura que se va a transformar, se debe considerar otro elemento básico para desarrollar esta transformación, siendo esta una constante, la cual se denomina constante de homotecia que viene a ser la escala en la cual se realiza la reproducción.

Tiene las siguientes propiedades:

• Los ángulos de las figuras por homotecia son iguales ya que tienen la misma medida.
• Los segmentos con paralelos.
• Las dimensiones de dos figuras por homotecia son directamente proporciónales; esta proporción es fijada por la constante de homotecia.

Aquellas figuras que no cumplen con la propiedad de ser paralelos los segmentos se les denomina figuras semejantes, a las que cumplen con todas las propiedades se les denomina figuras homoteticas.

En una homotecia de centro el punto O y razón k:

• Si k > 0, A y A′ están al mismo lado de O, y se dice que la homotecia es directa
• 
  

Si k < 0, A y A′ están a distinto lado de O, y se dice que la homotecia es inversa

A la figura ABCD le hemos aplicado una homotecia de centro O y razón k, con k > 0; homotecia directa.

A la figura ABC le hemos aplicado una homotecia de centro O y razón k, con k < 0; homotecia inversa..

''Teorema de Tales''

 

Existen dos teoremas relacionados con la geometría clásica que reciben el nombre de teorema de Tales, ambos atribuidos al matemático griego Tales de Mileto en el siglo VI a. C.

''los dos teoremas de tales''

Semicírculo que ilustra un teorema de Tales.

El primero de ellos explica esencialmente una forma de construir un triángulo semejante a uno previamente existente ("los triángulos semejantes son los que tienen iguales ángulos y sus lados homólogos proporcionales"). Mientras que el segundo desentraña una propiedad esencial de los circuncentros de todos los triángulos rectángulos ("encontrándose éstos en el punto medio de su hipotenusa"), que a su vez en la construcción geométrica es ampliamente utilizado para imponer condiciones de construcción de ángulos rectos. Si tres o más rectas paralelas son intersecadas cada una por dos transversales, los segmentos de las transversales determinados por las paralelas, son proporcionale

''Primer Teorema''

Una aplicación del teorema de Tales.

Como definición previa al enunciado del teorema, es necesario establecer que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre sí. El primer teorema de Tales recoge uno de los resultados más básicos de la geometría, al saber, que:

Teorema primero Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado. Tales de Mileto

Según parece, Tales descubrió el teorema mientras investigaba la condición de paralelismo entre dos rectas. De hecho, el primer teorema de Tales puede enunciarse como que la igualdad de los cocientes de los lados de dos triángulos no es condición suficiente de paralelismo. Sin embargo, la principal aplicación del teorema, y la razón de su fama, se deriva del establecimiento de la condición de semejanza de triángulos, a raíz de la cual se obtiene el siguiente corolario

Del establecimiento de la existencia de una relación de semejanza entre ambos triángulos se deduce la necesaria proporcionalidad entre sus lados. Ello significa que la razón entre la longitud de dos de ellos en un triángulo se mantiene constante en el otro.

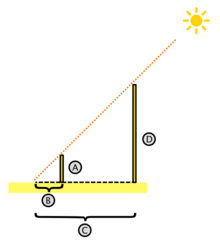
Por ejemplo, en la figura se observan dos triángulos que, en virtud del teorema de Tales, son semejantes. Entonces, del mismo se deduce a modo de corolario que el cociente entre los lados A y B del triángulo pequeño es el mismo que el cociente entre los lados D y C en el triángulo grande. Esto es, que como por el teorema de Tales ambos triángulos son semejantes, se cumple que:

Este corolario es la base de la geometría descriptiva. Su utilidad es evidente; según Heródoto, el propio Tales empleó el corolario de su teorema para medir la altura de lapirámide de Keops en Egipto. En cualquier caso, el teorema demuestra la semejanza entre dos triángulos, no la constancia del cociente.

Del primer teorema de Tales se deduce además lo siguiente (realmente es otra variante de dicho teorema, y, a su vez, consecuencia del mismo): Si las rectas A, B, C son paralelas y cortan a otras dos rectas R y S, entonces los segmentos que determinan en ellas son proporcionales.

''Segundo Teorema''

El segundo teorema de Tales de Mileto es un teorema de geometría particularmente enfocado a los triángulos rectángulos, lascircunferencias y los ángulos inscritos, consiste en el siguiente enunciado:

Teorema segundo Sea B un punto de la circunferencia de diámetro AC, distinto de A y de C. Entonces el triángulo ABC, es un triángulo rectángulo.

Aplicación (teorema de tales, segundo)

Construcción de tangentes (líneas rojas) a una circunferencia k desde un punto P, utilizando el «segundo teorema de Tales».

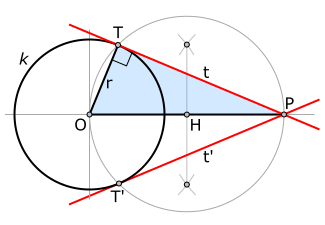
El “segundo teorema” (de Tales de Mileto) puede ser aplicado para trazar las tangentes a una circunferencia k dada, que además pasen por un punto P conocido y externo a la misma (véase figura ).

Se supondrá que una tangente cualquiera t (por ahora desconocida) toca a la circunferencia k en un punto T (también desconocido por ahora). Se sabe por simetría que cualquier radio r de la circunferencia k es perpendicular a la tangente del punto T que dicho radio define en la misma, por lo que concluimos que ángulo OTP es necesariamente recto.

Lo anterior implica que el triángulo OTP es rectángulo. Recordando el «corolario 2 del teorema segundo de Tales» podemos deducir que entonces el triángulo OTP es inscribible en una circunferencia de radio ½ de la hipotenusa OP del mismo.

Entonces marcando el punto H como punto medio de la hipotenusa OP y haciendo centro en el mismo, podemos dibujar una segunda circunferencia auxiliar (gris en la figura) que será la que circunscribe al triángulo OTP.

Esta última circunferencia trazada se intersecará con la circunferencia k en dos puntos T y T', estos son justamente los puntos de tangencia de las dos rectas que son simultáneamente tangentes a k y además pasan por el punto P, ahora ya conocidos los puntos T y T' solo basta trazar las rectas TP y T'P (rojas en la figura) para tener resuelto el problema.

Leyenda

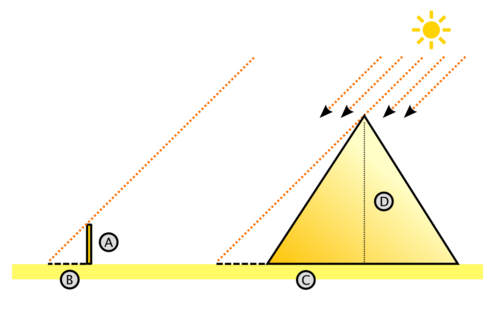
Según la leyenda (relatada por Plutarco¹ ), Tales de Mileto en un viaje a Egipto, visitó las pirámides de Guiza (las de Keops, Kefrén y Micerino), construidas varios siglos antes. Admirado ante tan portentosos monumentos de esta civilización, quiso saber su altura. De acuerdo a la leyenda, trató este problema con semejanza de triángulos (y bajo la suposición de que los rayos solares incidentes eran paralelos), pudo establecer una relación de semejanza (teorema primero de Tales) entre dos triángulos rectángulos, por un lado el que tiene por catetos (C y D) a la longitud de la sombra de la pirámide (conocible) y la longitud de su altura (desconocida), y por otro lado, valiéndose de una vara (clavada en el suelo de modo perfectamente vertical) cuyos catetos conocibles (A y B) son, la longitud de la vara y la longitud de su sombra. Realizando las mediciones en una hora del día en que la sombra de la vara sea perpendicular a la base de la cara desde la cual medía la sombra de la pirámide y agregando a su sombra la mitad de la longitud de una de las caras, obtenía la longitud total C de la sombra de la pirámide hasta el centro de la misma.

''PROPIEDADES DE POLIGONOS''

Polígono es la superficie plana encerrada dentro de un contorno formado por segmentos rectos unidos en sus extremos.

	Cada uno de los segmentos se denomina lado.
	El punto de unión de cada par de segmentos se denomina ángulo.
	El numero de lados, ( y por tanto de ángulos) ha de ser  mayor o igual a tres.

Polígono cruzado: Dos o mas lados se cortan. Los polígonos regulares estrellados son el caso más interesante. Polígono convexo: Si el segmento que une dos puntos cualesquiera del polígono es interior al polígono. Todos los ángulos interiores son menores de 180º. Si uno o más de los ángulos interiores es mayor de 180, el polígono es no convexo, o cóncavo. Polígono regular. Si tiene lados y ángulos iguales. El representado a la derecha es polígono equilátero,(lados iguales) pero no es regular (ángulos no iguales) Cruzado Reg Estrellado 9/2 Convexo No convexo (cóncavo) Regular convexo  Regular estrellado 5/2 No regular

 Algunas propiedades de los polígonos:

La suma de los ángulos interiores de un polígono        de n lados es 180(n-2).		En un polígono convexo la          suma de los ángulos exteriores es 360.

POLÍGONOS REGULARES CONVEXOS.

Como se ha indicado un polígono es regular si tiene sus lados iguales y sus ángulos iguales.

En la figura se muestran los elementos más importantes de un polígono regular.

Radio (r): segmento que une el centro con un vértice. Es el radio de la circunferencia circunscrita.

Apotema (a): Segmento que une el centro con el punto medio de un lado.

En un polígono regular de n lados:

Angulo central =360/n

Angulo interior = 180 - 360/n

Área = Perímetro x Apotema /2;   A = n· L · a /2 , ya que es el área de n triángulos  de base L y altura a

(L/2)² + a² = r²  por ser triangulo rectángulo L/2, r y a

CONSTRUCCIÓN DE POLÍGONOS REGULARES.

No todo polígono regular puede construirse con regla y compás. Más bien al contrario, algunos polígonos regulares pueden construirse de forma exacta. 

Se presentan algunos de los polígonos regulares construibles. Desde cada imagen se accede a su construcción.

N=3Triangulo Equilátero	N= 4 Cuadrado         .	N=5Pentágono Regular	N=6Hexágono Regular	N=8Octógono Regular.	N=10Decágono Regular	N=15Pentadecágono Regular	N=17Heptadecágono Regular

	Si un polígono regular de N lados es construible, también lo es el regular de 2N lados. Basta con trazar la circunferencia circunscrita y trazar la mediatriz de cada lado.
	Si un polígono de N lados es construible, también lo son los polígonos cuyo número de lados sea divisor de N. Uniendo los vértices correspondientes.

Desde Euclides se conocían construcciones geométricas con sólo regla y compás para polígonos regulares de 3, 4, 5 y 15 lados y todos los que se deducen de ellos por bisección:  6, 8, 10, 12,...  lados.

Gauss demostró, que son construibles los polígonos regulares con número de lados esto es, de lados  N=3 (n=0), N=5 (n=1), N=17 (n=2), N=257 (n=3), N=65537(n=4).

 También demostró la imposibilidad de la construcción de polígonos regulares de lados, 7,9,11,13,... en la que muchos  habían fracasado.

''CRITERIOS DE SEMEJANZA''

Triángulos semejantes

Dos triángulos son semejantes si sus ángulos son, respectivamente, iguales y sus lados homólogos son proporcionales.

Criterios de semejanza de triángulos

Para determinar si dos triángulos dados son semejantes bastaría con comprobar si verifican estas condiciones. Pero existen algunos principios que nos permiten determinar si dos triángulos son semejantes sin necesidad de medir y comparar todos sus lados y todos sus ángulos. Estos principios se conocen con el nombre de casos de semejanza de triángulos, o también:

Criterios de Semejanza de Triángulos

I. Primer criterio

Dos triángulos que tienen los tres ángulos iguales son semejantes entre sí.

A partir de este triángulo puedes obtener triángulos semejantes al original arrastrando el punto C o jugando con los valores de la escala. Observa que la medida de los ángulos, a pesar de todo, permanece constante.

II. Segundo criterio

Dos triángulos que tienen los tres lados proporcionales son semejantes entre sí.

El cociente obtenido de comparar los lados homólogos entre sí recibe el nombre de razón de semejanza.

III. Tercer criterio

Dos triángulos que tienen dos lados proporcionales y el ángulo comprendido entre ellos es igual, son semejantes entre sí.

De nuevo tienes aquí dos triángulos en posición de Tales. Como puedes comprobar, el ángulo B es común a ambos triángulos y los lados que lo forman son proporcionales entre sí.

''Ecuaciones Cuadraticas''

Definición:

Una ecuación de la forma ax2  +bx+c= 0  donde a,b y c son numeros reales y a es un numero diferente de cero.

Hay tres formas de hallar las raíces ( el o los valores de la variable) de las ecuaciones cuadráticas: 

1. Factorización Simple
2. Completando el Cuadrado
3. Fórmula Cuadrática
Factorización Simple:



 La factorización simple consiste en convertir la ecuación cuadrática en un producto de binomios. Luego, se busca el valor de x de cada binomio.
 
 
 
 
Ejemplo: Realizar la factorización simple de la ecuación
 x2 + 2x – 8  = 0          a = 1    b = 2    c = - 8

(x       )   (x       ) = 0                 [x ·x = x²]

( x +   )   (x  -   ) = 0 (x + 4 ) (x – 2) = 0                                        4 y –2     4 + -2 = 2                                                                     4 · -2 = -8       x + 4 = 0       x – 2 = 0     x + 4 = 0      x – 2 = 0 x = 0 – 4      x = 0 + 2 x = -4           x = 2                   Fórmula Cuadrática:Ejemplo: X2 + 2x – 8 = 0      a = 1, b = 2, c = -8      Este método es muy simple: hay que sustituir los valores de a, b y c de la ecuación cuadrática a la siguiente fórmula:         x = -2 ± 6           2 X

"SISTEMA DE ECUACIONES NO LINEALES "

Un sistema de ecuaciones es no lineal, cuando al menos una de sus ecuaciones no es de primer grado.

EJEMPLO :

La resolución de estos sistemas se suele hacer por el método de sustitución  , para ello se siguen los siguientes pasos :

1º Se despeja una incógnita en una de las ecuaciones, preferentemente en la de primer grado.y = 7 − x2º Se sustituye el valor de la incógnita despejada en la otra ecuación.x² + (7 − x)² = 25

3º Se resuelve la ecuación resultante.x² + 49 − 14x + x² = 252x² − 14x + 24 = 0x² − 7x + 12 = 04º Cada uno de los valores obtenidos se sustituye en la otra ecuación, se obtienen así los valores correspondientes de la otra incógnita.x = 3           y = 7 − 3        y = 4x = 4           y = 7 − 4        y = 3